ダミー変数を積極的に使用: Sample 2: 球座標から直座標への変換(FORTRAN)
言語の変更：
C版
■ 概要
式(1)は球座標から直座標に変換するための式です。sinやcosなどの関数が多くあり、いかにも重そうな計算です。よく見ると、繰り返しとなる計算があります。それを見つけて計算を少しでも軽くしましょう。
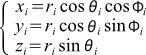... 式(1)
下の｢回答例」ボタンをクリックすれば、式(2)に回答例が表示されます。興味がある方はクリックする前にぜひ考えてみてください。
... 式(2)
Code 1は式(1)によってコーディングしたものです。Code 2は式(2)によってコーディングしたものです。配列xとyのサイズnは10,000とします。計算時間が非常に短いので、より正確な計算時間を得るためにこの計算は1000回まわします。
■ ソースコード
| ◆ Code 1 | ◆ Code 2 |
■ 計算時間の測定結果
Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | 平均 | 倍率 | |
|---|---|---|---|---|---|---|---|
| Code 1 | 2.07 | 2.06 | 2.06 | 2.06 | 2.06 | 2.06 | 1.24 |
| Code 2 | 1.65 | 1.67 | 1.67 | 1.67 | 1.67 | 1.67 | - |
■ 考察
Code 1はCode 2に1.24倍遅いという結果が得ました。
