計算量のオーダー
■ 計算量のオーダーとは
通常、数値計算にかかる時間は計算規模によります。規模が小さい場合は計算時間がかかりませんが、規模が大きくなると計算が重くなります。同じ計算規模でいかに計算時間を減らすかも大事ですが、計算規模が大きくなるときの計算時間の増え方を抑えることも大変重要です。つまり、計算規模が2倍になったときは計算時間が2倍になるか、4倍になるか、8倍になるか、それともそれ以上になるかは大規模の問題への適応性が決定されます。
計算規模を測る尺度は計算の種類によります。例えば、ソートの計算ではソートする集合の数、高速フーリエ変換の計算ではサンプリング数、有限要素法の計算では要素数。ここではそれらの尺度を簡単にサイズと呼び、Nという記号を用います。
計算規模と計算時間との関係は通常計算量のオーダーで表現されます。計算サイズが2倍になったら、計算時間も2倍になるときは計算量はサイズに比例するといいます。そのとき計算量のオーダーはO(N)と書きます。一方、サイズが2倍になったら、計算時間が22=4倍の場合は計算量のオーダーはO(N2)となります。同様に23=8倍ならO(N3)、21.5倍ならO(N1.5)となります。
■ 計算量のオーダーの重要性
小規模の計算しかしないうちなら、計算量のオーダーを気にすることはないかもしれません。しかし複雑なモデルを計算したり、高精度を求めて解析モデルをより細かく分割したりすると、計算規模が大きくなりがちです。そのときは計算量のオーダーを重要になります。計算量のオーダーの次数が大きいほど、大規模計算への適応性が悪くなります。具体的に計算量のオーダーの違いによる計算量の増え方の例を図1に示します。
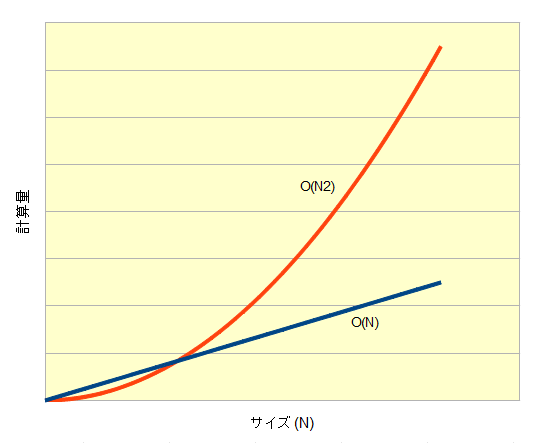
図1はO(N)とO(N2)のオーダーをもつ計算の計算量を、サイズNの関数として示したものです。サイズNが小さいうちはO(N)の方が計算量が大きいですが、ある一定のNからは逆転して、O(N2)の方が計算量が大きくなります。しかもNがどんどん大きくなると、O(N2)とO(N)との差が激しく開きます。実施している計算の計算量のオーダーがO(N2)よりO(N)の方が以下に有利なのかわかると思います。
■ 計算量のオーダーとアルゴリズム
大規模計算の際、計算量のオーダーを落とせば非常に有利ですが、計算量を落とすのは実は簡単ではありません。というか無理といっていいでしょう。しかし世の中にものすごく優秀なアルゴリズムがあり、それによって計算量のオーダーを1次程度落とせます。これらのアルゴリズムを作ったのはもちろん天才といえる方々です。我々のような凡人はアルゴリズムを作ることは無理なので、いかにいいアルゴリズムを知るかで、作った計算プログラムのスピードが変わります。
これ以降、管理者が知っているアルゴリズムをいくつか紹介いたします。その中に数値解析を行う上でよく現れる計算もありますので、知っておくと大変便利です。
