/*
Program to measure time to carry out matrix-vector product.
c(i) = sum(a(j,i)*b(j),j=1,...,n) for i=1,...,n
*/
#include <stdio.h>
#include <time.h>
int main()
{
int i, j;
printf("Matrix size Elapsed time [sec] \n");
for (int k=1; k<=30; k++) {
// Matrix size
int n = k*1000;
// Allocation
int **a, *b, *c;
a = new int*[n];
for (i=0; i<n; i++)
a[i] = new int[n];
b = new int[n];
c = new int[n];
// Initialization
for (j=0; j<n; j++)
for (i=0; i<n; i++)
a[j][i] = 1;
for (i=0; i<n; i++)
b[i] = 1;
// Start time
clock_t time0 = clock();
// Main calculation: matrix-vector product
for (i=0; i<n; i++) {
c[i] = 0;
for (j=0; j<n; j++) {
c[i] += a[j][i] * b[j];
}
}
// Finish time
clock_t time1 = clock();
// Output time
double eTime = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("%11d %15.7f\n",n, eTime);
// Deallocation
for (int i=0; i<n; i++)
delete[] a[i];
delete[] a;
delete[] b;
delete[] c;
}
return 0;
}
|
/*
Program to measure time to carry out matrix-vector product.
c(i) = sum(a(i,j)*b(j),j=1,...,n) for i=1,...,n
*/
#include <stdio.h>
#include <time.h>
int main()
{
int i, j;
printf("Matrix size Elapsed time [sec] \n");
for (int k=1; k<=30; k++) {
// Matrix size
int n = k*1000;
// Allocation
int **a, *b, *c;
a = new int*[n];
for (i=0; i<n; i++)
a[i] = new int[n];
b = new int[n];
c = new int[n];
// Initialization
for (j=0; j<n; j++)
for (i=0; i<n; i++)
a[j][i] = 1;
for (i=0; i<n; i++)
b[i] = 1;
// Start time
clock_t time0 = clock();
// Main calculation: matrix-vector product
for (i=0; i<n; i++) {
c[i] = 0;
for (j=0; j<n; j++) {
c[i] += a[i][j] * b[j];
}
}
// Finish time
clock_t time1 = clock();
// Output time
double eTime = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("%11d %15.7f\n",n, eTime);
// Deallocation
for (int i=0; i<n; i++)
delete[] a[i];
delete[] a;
delete[] b;
delete[] c;
}
return 0;
}
|
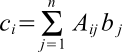 ... 式(1)
... 式(1)
.png)


