割り算を避ける: Sample 1: 基本(C)
■ 概要
ここでは割り算を掛け算に置き換えるときの計算時間の違いを調べます。計算するのは配列xを2で割るという単純な割り算です。
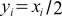
... 式(1)
式(1)を掛け算に変えるだけで非常に簡単ですが、とりあえず下の「回答例」ボタンをクリックすれば、式(2)に回答例が表示されます。

... 式(2)
Code 1は式(1)によってコーディングしたものです。Code 2は式(2)によってコーディングしたものです。配列xとyのサイズnは10,000とします。計算時間が非常に短いので、より正確な計算時間を得るためにこの計算は50,000回まわします。
このコードを見て不可解と思われる方はいるかもしれません。例えばCode 1ではtwoの変数を定義するときはわざわざjを足してその後jで引いたりしています(コード中の赤いフォントの部分を見てください)。これは「定数での割り算を掛け算に置き換える」というコンパイラーの最適化機能を無効にするための露骨なやり方です。このように書かないと、コンパイル時に「2で割り算」が自動的に「0.5と掛け算」に変えられてしまうからです。このサンプルでは余計な機能ですが、本当はとてもありがたい機能だとお伝えしておきましょう。
■ ソースコード
|
◆ Code 1
|
◆ Code 2
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int i,j;
int n = 10000, m = 50000;
// Initialization
double *x = new double[n];
double *y = new double[n];
for (i=0; i<n; i++) x[i] = rand();
// Start time
clock_t time0 = clock();
// Main calculation
for (j=0; j<m; j++) {
double two = j + 2.0 - j;
for (i=0; i<n; i++) {
y[i] = x[i] / two;
}
}
// Finish time
clock_t time1 = clock();
// Output time
double time = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("Time = %15.7f sec\n", time);
delete[] x;
delete[] y;
return 0;
}
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int i,j;
int n = 10000, m = 50000;
// Initialization
double *x = new double[n];
double *y = new double[n];
for (i=0; i<n; i++) x[i] = rand();
// Start time
clock_t time0 = clock();
// Main calculation
for (j=0; j<m; j++) {
double half = j + 0.5 - j;
for (i=0; i<n; i++) {
y[i] = x[i] * half;
}
}
// Finish time
clock_t time1 = clock();
// Output time
double time = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("Time = %15.7f sec\n", time);
delete[] x;
delete[] y;
return 0;
}
|
■ 計算時間の測定結果
Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。
表1 計算時間の測定結果(単位: sec)
|
1回目 |
2回目 |
3回目 |
4回目 |
5回目 |
平均 |
倍率 |
| Code 1 |
1.06 |
1.06 |
1.06 |
1.06 |
1.08 |
1.06 |
2.38 |
| Code 2 |
0.44 |
0.45 |
0.45 |
0.45 |
0.45 |
0.45 |
- |
■ 考察
表1の結果から割り算が掛け算の2.5倍弱遅いことが分かります。ただこれらの計算には掛け算と割り算の計算のほかにループの処理やメモリアクセスなどの計算コストもありますので、実際割り算と掛け算の比率はそれ以上あるはずです。
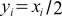 ... 式(1)
... 式(1)
 ... 式(2)
... 式(2)
