無駄な計算を無くす: Sample 3: 因数分解の利用(C)
■ 概要
このサンプルでは式(1)にしたがって配列a, b, cから配列xを計算します。式(1)では掛け算が4回、足し算が3回あります。このサンプルもきれいに因数分解できませんし、部分的な共通因子が二つあります。うまく括弧で共通因子をまとめられれば、掛け算は2回に減らせます。
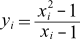
... 式(1)
下の「回答例」ボタンをクリックすれば、式(2)に回答例が表示されます。興味がある方はクリックする前にぜひ考えてみてください。

... 式(2)
Code 1は式(1)によってコーディングしたものです。Code 2は式(2)によってコーディングしたものです。配列xとyのサイズnは10,000とします。計算時間が非常に短いので、より正確な計算時間を得るためにこの計算は50,000回まわします。
■ ソースコード
|
◆ Code 1
|
◆ Code 2
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int i,j;
int n = 10000, m = 50000;
// Initialization
double *x = new double[n];
double *y = new double[n];
for (i=0; i<n; i++) x[i] = rand();
// Start time
clock_t time0 = clock();
// Main calculation
for (j=0; j<m; j++)
for (i=0; i<n; i++)
y[i] = (x[i]*x[i] - 1.0) / (x[i] - 1.0);
// Finish time
clock_t time1 = clock();
// Output time
double time = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("Time = %15.7f sec\n", time);
delete[] x;
delete[] y;
return 0;
}
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int i,j;
int n = 10000, m = 50000;
// Initialization
double *x = new double[n];
double *y = new double[n];
for (i=0; i<n; i++) x[i] = rand();
// Start time
clock_t time0 = clock();
// Main calculation
for (j=0; j<m; j++)
for (i=0; i<n; i++)
y[i] = x[i] + 1.0;
// Finish time
clock_t time1 = clock();
// Output time
double time = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("Time = %15.7f sec\n", time);
delete[] x;
delete[] y;
return 0;
}
|
■ 計算時間の測定結果
Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。
表1 計算時間の測定結果(単位: sec)
|
1回目 |
2回目 |
3回目 |
4回目 |
5回目 |
平均 |
倍率 |
| Code 1 |
3.23 |
3.23 |
3.23 |
3.23 |
3.39 |
3.26 |
1.91 |
| Code 2 |
1.70 |
1.70 |
1.70 |
1.72 |
1.70 |
1.70 |
- |
■ 考察
Code 1はCode 2に比べて1.91倍遅いという結果が得ました。
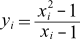 ... 式(1)
... 式(1)
 ... 式(2)
... 式(2)
