多重ループ: Sample 3: ダミー配列との併用(FORTRAN)

言語の変更： C版

■ 概要

このサンプルでは式(1)にしたがって配列aから2次元配列配列xを計算します。2次元配列だから、2重ループを使用して配列xを求めます。

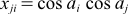... 式(1)

式(1)を素直にコーディングしたのはCode 1です。メイン計算では2つのループ、ループiとループj、を設けてその中に式(1)の右辺をそのまま計算しています。

前のサンプルと同様にCode 1ではcosの計算が2N²回ありますが、必要最低限はi=1からNまでのcos(a(i))なのでN回のはずです。しかしこのサンプルではcos(a(i))とcos(a(j))が必要であり、片方のcos(a(j))をループ外に出せたとしても、もう片方のcos(a(i))は出せないので、cosの計算が結局N²+N回までしか減らせませんでした。この改良でCode 1が若干高速化されてはいますが、まだ高速化が足りません。cosの計算が必要最低限のN回まで減らしたいです。

ループiとjを入れ替えても状況は変わらないことを確認できます。

Code 2はcos(a(i))の回数を極限のN回まで減らした例です。ここではダミー配列cos_aを使用しています。メイン計算の前にcos(a(i))の値を全部あらかじめ計算して、cos_a(i)に入れておきます。メイン計算にはcosの計算をせず、cos_aから必要なものを使うだけ。このようにすれば、cosの計算はN回だけで済みます。

ここで一つ注意点があります。Code 2はCode 1より高速ですが、使用メモリも配列cos_aの分だけ多いです。メモリに余裕があったらCode 2が通用しますが、メモリが厳しければCode 1を使用するしかありません。高速化と省メモリ化は一般的に正反対の関係にあることがよくあります。

■ ソースコード

◆ Code 1 ◆ Code 2

 
      program main
      implicit none
      real*8, allocatable :: a(:), x(:,:)
      real*8 time
      integer*8 time0, time1, dtime
      integer i, j, n
c
      n = 10000

c Initialization
      allocate(a(n), x(n,n))
      do i=1,n
        a(i) = rand()
      end do

c Start time
      call system_clock(time0)






c Main calculation
      do i=1,n
        do j=1,n
          x(j,i) = cos(a(i)) * cos(a(j))
        end do
      end do

c Finish time
      call system_clock(time1, dtime)

c Output time
      time = 1d0*(time1-time0)/dtime
      write(*,"(a7,f16.7)")"Time = ",time

      deallocate(a, x)
      end program

 
      program main
      implicit none
      real*8, allocatable :: a(:), x(:,:), cos_a(:)
      real*8 time
      integer*8 time0, time1, dtime
      integer i, j, n
c
      n = 10000

c Initialization
      allocate(a(n), x(n,n), cos_a(n))
      do i=1,n
        a(i) = rand()
      end do

c Start time
      call system_clock(time0)

c Preparation
      do i=1,n
        cos_a(i) = cos(a(i))
      end do

c Main calculation
      do i=1,n
        do j=1,n
          x(j,i) = cos_a(i) * cos_a(j)
        end do
      end do

c Finish time
      call system_clock(time1, dtime)

c Output time
      time = 1d0*(time1-time0)/dtime
      write(*,"(a7,f16.7)")"Time = ",time

      deallocate(a, x, cos_a)
      end program

■ 計算時間の測定結果

Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。

表1 計算時間の測定結果(単位: sec)
	1回目	2回目	3回目	4回目	5回目	平均	倍率
Code 1	8.44	8.46	8.46	8.52	8.63	8.50	13.8
Code 2	0.59	0.64	0.61	0.61	0.62	0.61	-

■ 考察

Code 1はCode 2に比べて13.8倍遅いという結果が得ました。

前: Sample 2: ループの順番(F)

次: メモリジャンプと高速化

多重ループ: Sample 3: ダミー配列との併用(FORTRAN)