行列とベクトルに関する計算: Sample 1: 行列と行列の掛け算(C)
■ 概要
行列と行列の掛け算は、特殊な場合を除いて、計算量のオーダーがO(N3)と決まっています。ここではある特殊な場合を考えます。つまり行列と行列を掛け算したあとにその結果の行列はまたベクトルを掛け算したい場合です。
式で書くと式(1)になります。この計算に必要なのはベクトルyだけであり、行列Cはyを計算するためだけであり、yが求まったらCは不要とします。
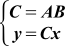
... 式(1)
式(1)を素直にコーディングしたのはCode 1になります。式(1)の前半はオーダーがO(N3)の行列と行列の掛け算、後半はオーダーがO(N2)の行列とベクトルの掛け算。
全体のオーダーは最大のオーダーで決まるので、O(N3)。
さて式(1)をまとめて書くと、y=(AB)xとなりますが、行列・ベクトルの掛け算の順番を入れ替えることはできるので、式(1)はy=A(Bx)とも書けます。さらに2つの式に分けると式(2)になります。
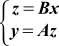
... 式(2)
式(2)でご注意していただきたいのは行列と行列の掛け算がなくなることです。その代わりに2つの行列とベクトルの掛け算がありますが、行列とベクトルの掛け算はオーダーがO(N2)なので、式(2)のオーダーは式(1)より一つ低く、O(N2)です。
この次にCode 1とCode 2を実際に実行するときにどのぐらい計算時間の差が出るかを見てみましょう。
■ ソースコード
|
◆ Code 1
|
◆ Code 2
|
#include <stdio.h>
#include <time.h>
int main()
{
int i, j, k;
printf("Matrix size Elapsed time [sec] \n");
for (int m=1; m<=20; m++) {
// Matrix size
int n = m*100;
// Allocation
double **a, **b, **c, *x, *y, *dum;
dum = new double[n*n];
a = new double*[n];
for (i=0; i<n; i++)
a[i] = dum + i*n;
dum = new double[n*n];
b = new double*[n];
for (i=0; i<n; i++)
b[i] = dum + i*n;
dum = new double[n*n];
c = new double*[n];
for (i=0; i<n; i++)
c[i] = dum + i*n;
x = new double[n];
y = new double[n];
// Initialization
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
a[i][j] = 1.0;
b[i][j] = 2.0;
}
x[i] = 1.0;
}
// Start time
clock_t time0 = clock();
// Main calculation 1: matrix-matrix product
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
c[i][j] = 0.0;
for (k=0; k<n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
// Main calculation 2: matrix-vector product
for (i=0; i<n; i++) {
y[i] = 0.0;
for (k=0; k<n; k++)
y[i] += c[i][k] * x[k];
}
// Finish time
clock_t time1 = clock();
// Output time
double eTime = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("%11d %15.7f\n",n, eTime);
// Deallocation
delete a[0]; delete b[0]; delete c[0];
delete[] a; delete[] b; delete[] c;
delete[] x; delete[] y;
}
return 0;
}
|
#include <stdio.h>
#include <time.h>
int main()
{
int i, j, k;
printf("Matrix size Elapsed time [sec] \n");
for (int m=1; m<=15; m++) {
// Matrix size
int n = m*1000;
// Allocation
double **a, **b, *x, *y, *z, *dum;
dum = new double[n*n];
a = new double*[n];
for (i=0; i<n; i++)
a[i] = dum + i*n;
dum = new double[n*n];
b = new double*[n];
for (i=0; i<n; i++)
b[i] = dum + i*n;
x = new double[n];
y = new double[n];
z = new double[n];
// Initialization
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
a[i][j] = 1.0;
b[i][j] = 2.0;
}
x[i] = 1.0;
}
// Start time
clock_t time0 = clock();
// Main calculation 1: matrix-vector product
for (i=0; i<n; i++) {
z[i] = 0.0;
for (k=0; k<n; k++)
z[i] += b[i][k] * x[k];
}
// Main calculation 2: matrix-vector product
for (i=0; i<n; i++) {
y[i] = 0.0;
for (k=0; k<n; k++)
y[i] += a[i][k] * z[k];
}
// Finish time
clock_t time1 = clock();
// Output time
double eTime = (double)(time1-time0)/CLOCKS_PER_SEC;
printf("%11d %15.7f\n",n, eTime);
// Deallocation
delete a[0]; delete b[0];
delete[] a; delete[] b;
delete[] x; delete[] y; delete[] z;
}
return 0;
}
|
■ 計算時間の測定結果
Code 1とCode 2を実行したときの計算時間をそれぞれ青線と赤線で図1に示します。
Code 2の計算時間はCode1に比べて非常に短いので、Code 1と同じサイズNで測定すると、計算時間が測定できません。ここではCode 2のサイズNをCode 1より大きい範囲にしています。
図1 測定時間
■ 考察
図1より解かりますが、Code 1の計算時間はCode 2より非常に長いです。しかもサイズNが大きくなるにつれて、その差がどんどん開きます。ちなみにN=2000ではCode 1の計算時間は既にCode 2の5000倍程度になっています。Code 1をNが10000まで計算してもよいですが、1日ぐらいかかりそうなので、止めました。この結果より、O(N3)の恐ろしさを実感できるのではないでしょうか。
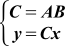 ... 式(1)
... 式(1)
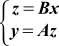 ... 式(2)
... 式(2)
.png)
